Question

If the velocity of blood flow in the aorta is normally about 0.32 m/s, what beat frequency would you expect if 4.40-MHz ultrasound waves were directed along the flow and reflected from the red blood cells? Assume that the waves travel with a speed of 1540 m/s .

Answer 1

The beat frequency is 0.0019 MHz.

Step-by-step explanation:

Given that,

Velocity = 0.32 m/s

Frequency = 4.40 MHz

Speed of wave = 1540 m/s

We need to calculate the frequency

Case (I),

Observer is moving away from the source

Using Doppler's effect

`f'=(v-v')/(v)f`

Where, v' = speed of observer

Put the value into the formula

`f'=(1540-0.32)/(1540)*4.40`

`f'=4.399\ MHz`

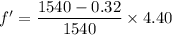
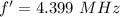
Case (II),

Cell is as the source of sound of frequency f' and it moving away from the observer.

Using formula of frequency

`f''=(v-v_(s))/(v+v_(s))* f`

`f''=(1540-0.32)/(1540+0.32)*4.399`

`f''=4.3971\ MHz`

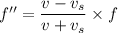
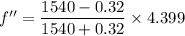
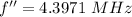
We need to calculate the beat frequency

`\Delta f= f'-f''`

`\Delta f=4.399-4.3971=0.0019\ MHz`

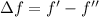
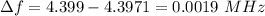
Hence, The beat frequency is 0.0019 MHz.