Question

How do you find the sine and tangent of an angle if you are given the cosine?

Teacher said I wasn't allowed to use sohcahtoa, or even make a triangle out of an angle, he said it was only an angle, he also said I can make an example of the angle. Any help?

Answer 1

• sin = √(1 -cos²)
• tan = (√(1 -cos²))/cos

Explanation:

`\displaystyle\sin^2{\theta}+\cos^2{\theta}=1 \qquad\text{Pythagorean identiy}\\\\sin(\theta)=\sqrt{1-\cos^2{\theta}} \qquad\text{solved for sine}\\\\tan(\theta)=(sin(\theta))/(cos(\theta))=\frac{\sqrt{1-\cos^2{\theta}}}{cos(\theta)}`

_____

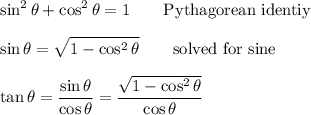
If you draw a triangle with a hypotenuse of 1 and an "adjacent" leg of "cos", then using the Pythagorean theorem, you can see that the "opposite" leg will be √(1-cos²) and the tangent will be (√(1-cos²))/cos. Whether or not you're allowed to draw such a triangle on paper, you can certainly do it in your mind.