Question

For what values of x is x2+2x=24 true?

Answer 1

The answer is C). 4 and-6

Explanation:

Answer 2

`x=-6` and
`x=4`

Explanation:

We must solve the quadratic equation to find the values of x that satisfy equality

`x^2+2x=24`

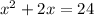
Subtract 24 on both sides of equality

`x^2+2x-24=24-24`

`x^2+2x-24=0`

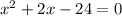
Now we factor the quadratic equation

Identify two numbers that when you add them you get as a result 2 and when you multiply them you get as a result -24

The numbers sought are: 6 and -4

So the factors are:

`(x+6)(x-4)=0`

Finally note that the solutions are:

`x=-6` and
`x=4`