Question

Suppose the half-life of a material is 10 days. You have one 1 kg of the material today. How much of the material would you have after 10 days and 20 days, respectively?

Answer 1

0.50 kg of the material would be left after 10 days.

0.25 kg of the material would be left after 20 days.

Explanation:

We have been given that the half-life of a material is 10 days. You have one 1 kg of the material today. We are asked to find the amount of material left after 10 days and 20 days, respectively.

We will use half life formula.

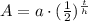`A=a\cdot((1)/(2))^{(t)/(h)}`, where,

A = Amount left after t units of time,

a = Initial amount,

t = Time,

h = Half-life.

`A=1\text{ kg}\cdot((1)/(2))^{(10)/(10)}`

`A=1\text{ kg}\cdot((1)/(2))^(1)`

`A=1\text{ kg}\cdot(1)/(2)`

`A=0.5\text{ kg}`

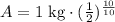
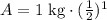
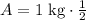
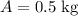
Therefore, amount of the material left after 10 days would be 0.5 kg.

`A=1\text{ kg}\cdot((1)/(2))^{(20)/(10)}`

`A=1\text{ kg}\cdot((1)/(2))^(2)`

`A=1\text{ kg}\cdot(1^2)/(2^2)`

`A=1\text{ kg}\cdot(1)/(4)`

`A=0.25\text{ kg}`

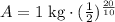
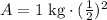
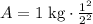
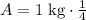
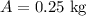
Therefore, amount of the material left after 20 days would be 0.25 kg.