Question

The given measurements may or may not determine a triangle. If not, then state that no triangle is formed. If a triangle is formed, then use the Law of Sines to solve the triangle, if it is possible, or state that the Law of Sines cannot be used. B = 111°, c = 8, b = 12

Answer 1

h=(a)(sinC)=19(sin37)

That means h ≈11.43

Since c<h, There is no triangle

Answer 2

The Dimensions of triangle are

B=111°, c=8 , b=12

First we will use Cosine Law to Determine , measurement of third side.

`\cos B=(b^2+c^2-a^2)/(2bc)\\\\ \cos 111^(\circ)=((12)^2+(8)^2-a^2)/(2 * 12 * 8)\\\\-0.35836=(144+64-a^2)/(192)\\\\-68.80=208-a^2\\\\a^2=208+68.80\\\\a^2=276.80\\\\a=√(276.80)\\\\a=16.64`

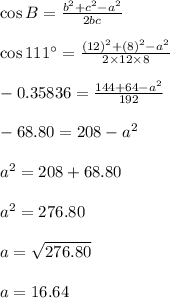
To Form a Triangle ,Sum of two sides of a triangle should be greater than third side.

a=16.64 , b=12, c=8

Angle in front of Side 12 unit has measure 111°, which is an Obtuse Angle.Also Length of Other side is 16.64 unit, so This Angle should also be greater than 111°, But sum of three angles of Triangle is equal to 180°.So, This triangle is not Possible.