Question

Solve by using the measurements ∠PQR = 90°, ∠QRP = 80°, and r = 15. Round measures of sides to the nearest tenth and measures of angles to the nearest degree.

Answer 1

q ≈ 15.2

p ≈ 2.5

Explanation:

Given that:

• ∠PQR = 90°
• ∠QRP = 80°
• r = 15

We need to find the length of side q and p

Use the sine law to find out q, we have:

sin(QRP) =
`(r)/(q)`

<=> sin(80°) =
`(r)/(q)`

<=> q =
`(r)/(sin(80))` =
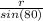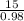`(15)/(0.98)` ≈ 15.2

Because PQR is a right triangle, so we use pytagon theorem to find p

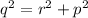
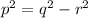
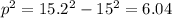
`q^(2) = r^(2) + p^(2)`

<=>
`p^(2) = q^(2) - r^(2)`

<=>
`p^(2) = 15.2^(2) - 15^(2) = 6.04 \\`

<=> p =
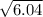`√(6.04)` ≈ 2.5

Answer 2

Good evening ,

___________________

Explanation:

Look at the photo below for the answer.

:)