Answer: 756
Explanation:
Given : The proportion of adults over 50 never graduated from high school. = 0.23
Margin of error : E=0.03
Significance level :

Critical value :
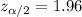
The formula to find the sample size is given by:_
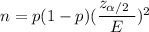
i.e.

Hence, the required minimum sample size = 756