Answer with explanation:
Given : The critical path for the project has an expected duration of 112 days, and a standard deviation of 5 days.
i.e.
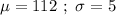
We assume that this a normal distribution.
Let x be the random variable that represents the time duration to complete the project.
z-score :
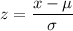
For x= 115
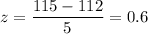
P-value :
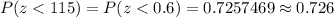
Thus, the probability of finishing on time if the due date is 115 days is 0.726.
Also, for x= 120
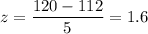
P-value :
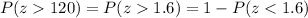
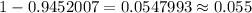
Hence, the probability that they will have to pay the penalty is 0.055 .