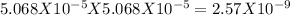Question

The solubility of barium carbonate, BaCO3, is 0.0100 g/L. Its molar mass is 197.3 g/mol. What is the Ksp of barium carbonate?Express your answer numerically.

Answer 1

Ksp =
`2.57X10^(-9)`

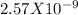
Step-by-step explanation:

Molar solubility of barium carbonate will be obtained by dividing the given solubility (in g/L) with molar mass of barium carbonate

molar solubility =
`(solubility)/(molarmass)=(0.01)/(197.3)=5.068X10^(-5)M`

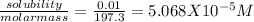
The barium carbonate will undergo dissociation as:

`BaCO_(3)------>Ba^(+2)+CO_(3)^(-2)`

Ksp of barium carbonate will be

Ksp =
`[Ba^(+2)][CO_(3)^(-2)]`

If solubility of barium carbonate is "s"

The concentration of each ion will be "s"

Hence the expression becomes

Ksp = s²

where

s = molar solubility = 5.068 X10⁻⁵

Ksp =
`5.068X10^(-5)X5.068X10^(-5)=2.57X10^(-9)`