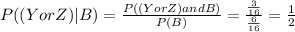Question

PLEASE HELP! The table shows the number of championships won by the baseball and softball leagues of three youth baseball divisions organized by age groups.

Baseball League (B) Softball League (S)

Ages 7 – 9 (X) 3 7

Ages 10 – 12 (Y) 2 2

Ages 13 – 15 (Z) 1 1



Question 1:
If the winning team plays in the Ages 10 - 12 division, find the probability that the team is in the Baseball League. Answer in terms of a reduced fraction.

P(B|Y) =

Question 2:
If the winner is in Baseball League, find the probability that the winning team is in either the Ages 10 - 12 division or the Ages 13 - 15 division. Answer in terms of a reduced fraction. (this is a three part question)

A. P(Y | B) =
B. P(Z | B) =
C. P(Y or Z |B) =



Please answer ALL of these questions. Good Luck!

Answer 1

Question 1:
`P ( B | Y ) = ( P ( B and Y))/( P (Y)) = ( (2)/(16))/( (4)/(16)) = (1)/(2)`

Question 2:

A.
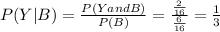
`P ( Y | B ) = ( P(Y and B) )/( P(B) ) = ( (2)/(16) )/( (6)/(16) ) = (1)/(3)`

B.
`P( Z | B ) = ( P ( Z and B))/( P (B))= ( (1)/(16) )/( (6)/(16) ) = (1)/(6)`

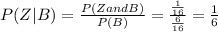
C.
`P((Y or Z)|B) = ( P ((Y or Z) and B))/(P(B))= ( (3)/(16))/( (6)/(16))= (1)/(2)`

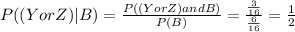
Explanation:

Conditional probability is defined by

`P(A|B)= (P(A and B))/(P(B))`

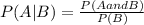
with P(A and B) beeing the probability of both events occurring simultaneously.

Question 1:

B: Baseball League Championships won, beeing

`P ( B ) = ( 6 )/(16)`

Y: Championships won by the 10 - 12 years old, beeing

`P ( Y)= ( 4 )/( 16 )`

then

P( B and Y)= \frac{ 2 }{ 16 }[/tex]

By definition,

`P ( B | Y ) = ( P ( B and Y))/( P (Y)) = ( (2)/(16) )/( (4)/(16) )  = (1)/(2)`

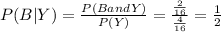
Question 2.A:

Y: Championships won by the 10 - 12 years old, beeing

`P ( Y)= ( 4 )/( 16 )`

B: Baseball League Championships won, beeing

`P ( B ) = ( 6 )/(16)`

then

P( B and Y)= \frac{ 2 }{ 16 }[/tex]

By definition,

`P ( Y | B ) = ( P(Y and B) )/( P(B) ) = ( (2)/(16) )/( (6)/(16) ) = (1)/(3)`

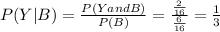
Question 2.B:

Z: Championships won by the 13 - 15 years old, beeing

`P ( Z)= ( 1 )/( 16 )`

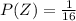
B: Baseball League Championships won, beeing

`P ( B ) = ( 6 )/(16)`

then

P( Z and B)= \frac{ 1 }{ 16 }[/tex]

By definition,

`P( Z | B ) = ( P ( Z and B))/( P (B))= ( (1)/(16) )/( (6)/(16) ) = (1)/(6)`

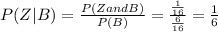
Question 3.B

Y: Championships won by the 10 - 12 years old, beeing

`P ( Y)= ( 4 )/( 16 )`

Z: Championships won by the 13 - 15 years old, beeing

`P ( Z)= ( 1 )/( 16 )`

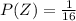
then

`P (Y or Z) = P(Y) + P(Z) = (6)/(16)`

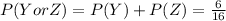
B: Baseball League Championships won, beeing

`P ( B ) = ( 6 )/(16)`

so

`P((YorZ) and B)= (3)/(16)`

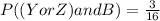
By definition,

`P((Y or Z)|B) = ( P ((Y or Z) and B))/(P(B))= ( (3)/(16))/( (6)/(16))= (1)/(2)`