Answer:
The power consumed by the air filter is 9.936 watts
Step-by-step explanation:
It is given that, the secondary coil of a step-up transformer provides the voltage that operates an electrostatic air filter.
Turn ratio of the transformer,

Voltage of primary coil,
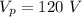
Current in the secondary coil,

The power consumed by the air filter is :
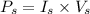 ...........(1)
...........(1)
For a transformer,
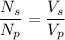
So,

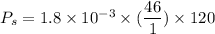
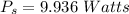
So, the power consumed by the air filter is 9.936 watts. Hence, this is the required solution.