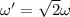Question

A DVD is initially at rest. It then begins to rotate counterclockwise with constant angular acceleration . After the DVD has rotated through an angle , its angular speed is . If instead the DVD is initially at rest and its constant angular acceleration is doubled to after the DVD has rotated through the same angle, its angular speed will be

Answer 1

`\omega' = \sqrt2\omega`

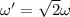
angular speed is increased by
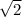`\sqrt2` factor

Step-by-step explanation:

As we know that the angular acceleration is constant and initially the disc is at rest

so here we can say by kinematics

`\omega^2 = \omega_0^2 + 2\alpha \theta`

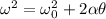
here we know that angle turned by the disc is
`\theta`

now we have

`\omega = √(2\alpha\theta)`

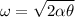
now the same disc start from rest with double angular acceleration and turned by same angle then final angular speed is given as

`\omega' = √(2(2\alpha)\theta)`

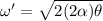
so here we have

`\omega' = \sqrt2\omega`