Answer:
24 hours
Explanation:
Let t represent time taken by Carl's son to complete the work alone.
Part of garden planted by Carl's son in 1 hour would be
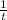 .
.
We have been given that Carl can plant his garden in 8 hours, so part of garden planted by Carl in 1 hour would be
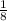 .
.
We have been given that Carl can plant his garden in 6 hours with his son, so part of garden planted by Carl and his son in 1 hour would be
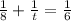 .
.
Now, let us solve for t.
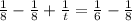
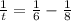
Make a common denominator:

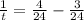
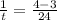
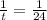
Cross multiply:
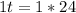
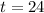
Therefore, it will take Carl's son 24 hours to plant the garden alone.