Question

The Acme Company manufactures widgets. The distribution of widget weights is bell-shaped. The widget weights have a mean of 60 ounces and a standard deviation of 7 ounces. Use the Standard Deviation Rule, also known as the Empirical Rule. Suggestion: sketch the distribution in order to answer these questions.(a) 95% of the widget weights lie between and (b) What percentage of the widget weights lie between 12 and 57 ounces?(c) What percentage of the widget weights lie above 30 ?

Answer 1

Explanation:

Given that the Acme Company manufactures widgets, which have a mean of 60 ounces and a standard deviation of 7 ounces

We know that 95% of the area lie between -2 and 2 std deviations from the mean.

i.e. Probability for lying in the middle of 95%

Z score
`(60+7(-2), 60+7(2))\\=(46, 74)`

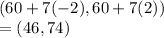
Between 46 and 74 oz.

b) Between 12 and 57

convert into Z score

`((12-60)/(7) <z<(57-60)/(7))`

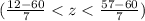
P(-6.86<z<-0.43)

=0.5-0.1664=0.3336

c) X<30 gives Z<-4.83

i.e. P(X<30) =0.00