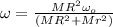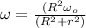Question

A disk of mass M and radius R rotates at angular velocity ω0. Another disk of mass M and radius r is dropped on top of the rotating disk such that their centers coincide. Both disks now spin at a new angular velocity ω. What is ω?

Answer 1

`\omega = ((R^2\omega_o)/((R^2 + r^2))`

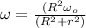
Step-by-step explanation:

As we know that there is no external torque on the system of two disc

then the angular momentum of the system will remains conserved

So we will have

`L_i = L_f`

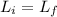
now we have

`L_i = ((1)/(2)MR^2)\omega_o`

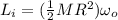
also we have

`L_f = ((1)/(2)MR^2 + (1)/(2)Mr^2)\omega`

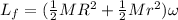
now from above equation we have

`((1)/(2)MR^2)\omega_o  = ((1)/(2)MR^2 + (1)/(2)Mr^2)\omega`

now we have

`\omega = (MR^2\omega_o)/((MR^2 + Mr^2))`

`\omega = ((R^2\omega_o)/((R^2 + r^2))`