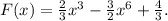Answer:
The expression for the function is F(x) = (2/3)x^3-(3/2)x^6+4/3.
Explanation:
If we use indefinite integration we can find the family of antiderivatives of f(x). This means that
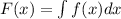
is an antiderivative of f(x). The, using the properties of the integral:
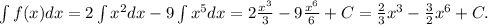
Here, C stands for a generic real constant. We use the data F(1)=0 in order to find the exact value of C. Notice that
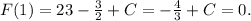
Then,
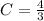 and
and