Answer:
Maximum height reached by the ball is 32 meters.
Step-by-step explanation:
It is given that,
If a baseball is project upwards from the ground level with an initial velocity of 32 feet per second, then it's height is a function of time. The equation is given as :
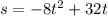 ...........(1)
...........(1)
t is the time taken
s is the height attained as a function of time.
Maximum height achieved can be calculated as :
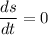

-16 t + 32 = 0
t = 2 seconds
Put the value of t in equation (1) as :

s = 32 meters
So, the maximum height reached by the ball is 32 meters. Hence, this is the required solution.