Step-by-step explanation:
The concentration of salt after t minutes is given by :
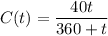
A tank contains 9000 L of pure water. Brine that contains 40 g of salt per liter of water is pumped into the tank at a rate of 25 L/min.
We need to find the concentration approach at

So,
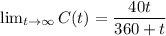
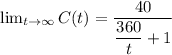
Put


Since,

C(t) = 40 g/L
So, at
 the concentration approaches to 40 g/L. Hence, this is the required solution.
the concentration approaches to 40 g/L. Hence, this is the required solution.