Question

Halleys comet has period of 75.3 years. Using Kepler’s third law, find it’s semimajor axis expressed in astronomical units?

Answer 1

Answer: 17.83 AU

Step-by-step explanation:

According to Kepler’s Third Law of Planetary motion “The square of the orbital period of a planet is proportional to the cube of the semi-major axis (size) of its orbit”.

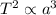`T^(2)\propto a^(3)` (1)

Talking in general, this law states a relation between the orbital period
`T` of a body (moon, planet, satellite, comet) orbiting a greater body in space with the size
`a` of its orbit.

However, if
`T` is measured in years, and
`a` is measured in astronomical units (equivalent to the distance between the Sun and the Earth:
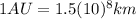`1AU=1.5(10)^(8)km`), equation (1) becomes:

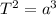`T^(2)=a^(3)` (2)

This means that now both sides of the equation are equal.

Knowing
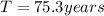`T=75.3years` and isolating
`a` from (2):

`a=\sqrt[3]{T^(2)}=T^(2/3)` (3)

`a=(75.3years)^(2/3)` (4)

Finally:

`a=17.83AU` (5)