Question

Weekend​ Warriors, Inc., has 35​% debt and 65​% equity in its capital structure. The​ firm's estimated​ after-tax cost of debt is 8​% and its estimated cost of equity is 13​%. Determine the ​firm's weighted average cost of capital ​(WACC​).

Answer 1

WACC 11.25%

Step-by-step explanation:

`WACC = K_e((E)/(E+D)) + K_d(1-t)((D)/(E+D))`

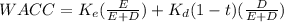
cost of equity:

`K_e= 0.13`

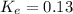
equity:

`(E)/(E+D)=0.65`

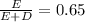
after tax cost of debt:

`K_d(1-t) = 0.08`

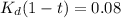
debt to equity:

`(D)/(E+D)=0.35`

`WACC = 0.13(0.65) + 0.08(0.35)`

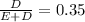
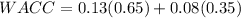
WACC = 0.11250 = 11.25%

Notice that we multiply the cost of capital by the percent of the capital structure which is equity.

And we multiply the cost of debt by the part of debt in the capital structure