Question

At some instant and location, the electric field associated with an electromagnetic wave in vacuum has the strength 70.5 V/m. Find the magnetic field strength, the energy density, and the power flow per unit area, all at the same instant and location.

Answer 1

The magnetic field strength, the energy density, and the power flow per unit area are
`2.35*10^(-7)\ T`,
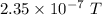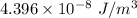`4.396*10^(-8)\ J/m^3` and 13.18 W/m².

Step-by-step explanation:

Given that,

Electromagnetic wave strength E= 70.5 V/m

(I). We need to calculate the magnetic field strength

Using formula of Electromagnetic wave strength

`c= \dfrca{E}{B}`

`B=(E)/(c)`

`B=(70.5 )/(3*10^(8))`

`B=2.35*10^(-7)\ T`

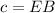
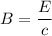
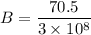
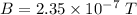
(II). We need to calculate the energy density

Using formula of energy density

`\mu_(total)=\mu_(E)+\mu_(B)`

`\mu_(total)=(1)/(2)\epsilon_(0)E^2+(1)/(2)(B^2)/(\mu_(0))`

`\mu_(total)=(1)/(2)*8.85*10^(-12)*(70.5)^2+(1)/(2)*((2.35*10^(-7))^2)/(4\pi*10^(-7))`

`\mu_(total)=4.396*10^(-8)\ J/m^3`

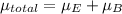
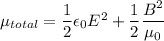
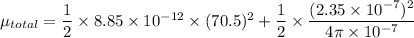
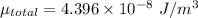
(III). We need to calculate the power flow per unit area

Using formula of poynting vector

`S=(1)/(\mu_(0))EB`

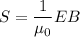
Put the value into the formula

`S=(1)/(4\pi*10^(-7))*70.5*2.35*10^(-7)`

`S=13.18\ W/m^2`

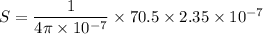
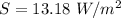
Hence, The magnetic field strength, the energy density, and the power flow per unit area are
`2.35*10^(-7)\ T`,
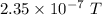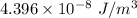`4.396*10^(-8)\ J/m^3` and 13.18 W/m².