Question

The electric potential at the origin of an xy-coordinate system is 40 V. A -8.0-μC charge is brought from x = +∞ to that point. What is the electric potential energy of this charge at the origin?

Answer 1

The electric potential energy of the charge at the origin is -320 μJ.

Step-by-step explanation:

The electric potential energy of a point charge is given by the equation:

Electric potential energy = (charge) * (electric potential)

In this case, the charge is -8.0 μC and the electric potential is 40 V. Therefore, the electric potential energy of the charge at the origin is:

Electric potential energy = (-8.0 μC) * (40 V) = -320 μJ

Answer 2

-320 μJ.

Step-by-step explanation:

Consider a point with an electrical charge of
`q`. Assume that
`V` is the electrical potential at the position of that charge. The electrical potential of that point charge will be equal to:

`\text{Potential Energy} = q \cdot V`.

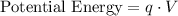Keep in mind that since both
`q` and
`V` might not be positive, the size of the electrical potential energy might not be positive, either.

For this point charge,

• 
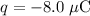  `q = \rm -8.0\; \mu C`; (that's -8.0 microjoules, which equals to
  `\rm -8.0* 10^(-6)\; J`)
• 
  `V = \rm 40\; V`.

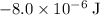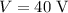Hence its electrical potential energy:

`\text{Potential Energy} = q\cdot V = \rm (-8.0\; \mu C) * 40\; V = -320\; \mu J`.

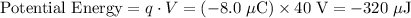Why is this value negative? The electrical potential energy of a charge is equal to the work needed to bring that charge from infinitely far away all the way to its current position. Also, negative charges are attracted towards regions of high electrical potential. Bringing this
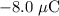`\rm -8.0\; \mu C` negative charge to the origin will not require any external work. Instead, this process will release 320 μJ of energy. As a result, the electrical potential energy is a negative value.