Question

nsider three resistors with unequal resistances connected in series to a battery. Which of the following statements are true?Check all that apply.Check all that apply.The algebraic sum of the voltages across the three resistors is equal to the voltage supplied by the battery.The equivalent resistance of the combination of resistors is greater than the resistance of any one of the three resistors.The algebraic sum of the currents flowing through each of the three resistors is equal to the current supplied by the battery.The equivalent resistance of the combination of resistors is less than the resistance of any one of the three resistors.The voltage across each of the resistors is the same and is equal in magnitude to the voltage of the battery.The current flowing through each of the resistors is the same and is equal to the current supplied by the batt

Answer 1

The algebraic sum of the voltages across the three resistors is equal to the voltage supplied by the battery.

The equivalent resistance of the combination of resistors is greater than the resistance of any one of the three resistors.

The current flowing through each of the resistors is the same and is equal to the current supplied by the battery.

Step-by-step explanation:

As we know that when three resistors are connected in series with unequal magnitude

then we have

`R_(eq) = R_1 + R_2 + R_3`

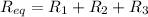
now the we can say that the equivalent resistance of all three resistors is more than any one of the individual resistance

now since they all are connected in series so the current must be same in all resistance which is same as the current flowing through the battery

This current is given as

`i = (V)/(R_1 + R_2 +R_3)`

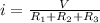
now we know that voltage across each resistance is given by

`V_1 = i R_1`

`V_2 = i R_2`

`V_3 = i R_3`

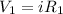
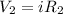
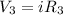
so here sum of voltage across each resistance is equal to the total voltage of the battery