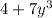Answer:
Width =
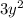
Length =
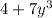
Explanation:
Area of the rectangle =
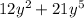
Width of the rectangle is greatest common monomial factor of
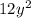 and
and
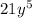 . Monomial means consisting of a one term only. Terms in an algebraic expression are distinguished by symbols of addition and subtraction. So, in expression of Area there are 2 terms. Factorizing the expression of Area will give us the width and length of the rectangle as shown below:
. Monomial means consisting of a one term only. Terms in an algebraic expression are distinguished by symbols of addition and subtraction. So, in expression of Area there are 2 terms. Factorizing the expression of Area will give us the width and length of the rectangle as shown below:
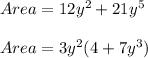
Since, Area of a rectangle is the product of its length and width, and the monomial factor represents the width, we can write:
Width =
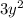
Length =