It looks like you're supposed to show
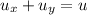
We have
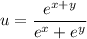
In the numerator, we have
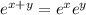 , so that the derivative wrt either
, so that the derivative wrt either
 or
or
 is simply
is simply
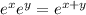 . In the denominator, either
. In the denominator, either
 or
or
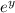 vanishes.
vanishes.
Differentiating wrt
 gives, by the quotient rule,
gives, by the quotient rule,
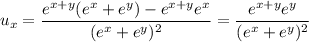
Similarly, differentiating wrt
 gives
gives
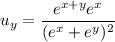
Then

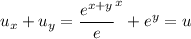
as required.