Answer:
12
Explanation:
note that x³ + 8 is a sum of cubes and factors as
x³ + 8 = (x + 2)(x² - 2x + 4), thus
lim x → - 2
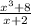
= lim x → - 2
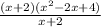
Cancel factor (x + 2) on numerator/denominator
= lim x → - 2 (x² - 2x + 4) ← evaluate by direct substitution
= (- 2)² - 2(- 2) + 4 = 4 + 4 + 4 = 12