Question

​how many solutions 2x+3y=−6 3x−4y=−12 ​

Answer 1

the correct answer is A. This system has no solutions. It is not possible for two x minus three y to equal both negative six and nine at the same time.

Explanation:

i hope this helps

Answer 2

Here is your system of equations:

`\left \{ {{2x+3y=-6} \atop {3x-4y=-12}} \right.`

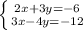
When solving a system, you can either substitute or eliminate. I am going to eliminate because you can only substitute when there are answer choices.

When eliminating, you need either x or y to be the same or opposite(sign). I am going to eliminate y, whuch means 3y and -4y has to have the same number. To make them the same, I will multiply the two numbers because multiplying two numbers is an easier way to find a common multiple.

`3 * 4 = 12`

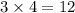
That means they both have to be changed so that their value is 12.

`2x+3y=-6 \\ \\ 3 * ?=12 \\ ?=4`

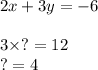
You have to multiply the first equation by 4.

`2x+3y=-6 \rightarrow 8x+12y=-24`

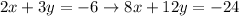
For the second equation, I will have to multiply by 3 because:

`3x-4y=-12 \\ \\-4 * ?=-12 \\?=3`

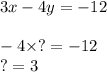
Multiply the second equation by 3:

`3x-4y=-12 \rightarrow 9x-12y=-36`

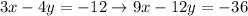
Here is your new system of equations:

`\left \{ {{8x+12y=-24} \atop {9x-12y=-36}} \right.`

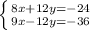
Add:

`{8x+12y=-24} \\{9x-12y=-36} \\ \\ 17x=-60`

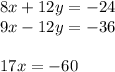
y is eliminated because when a number is added/subtracted by its opposite, it's cancelled out.

Although the case is different, remember:

NEGATIVES

• Negative(-) times(×) negative(-) = positive(+)
• Negative(-) times(×) positive(+) = negative(-)
• Negative(-) divided(÷) by positive(+) = negative(-)
• Negative(-) divided(÷) by negative(-) = positive(+)

POSITIVES

• Positive(+) times(×) positive(+) = positive(+)
• Positive(-) times(×) negative(-) = negative(-)
• Positive(+) divided(÷) by positive(+) = positive(+)
• Positive(+) divided(÷) by negative(-) = negative(-)

Now you need to divide both sides by 17 to leave x alone.

`(17x)/(17) =(-60)/(17) \\ \\ x=-(60)/(17)`

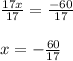
Since x has a value, that means y also does. That also means the answer to your question is one solution.