Question

What is the sum of all real numbers x that are not in the domain of the function f(x) = \frac{1}{x^2-7} + \frac{1}{x^3-8} + \frac{1}{x^4-9}~?

Answer 1

The sum of all real numbers x that are not in the domain of the function f(x) is 2.

Explanation:

The given function is

`f(x)=(1)/(x^2-7)+(1)/(x^3-8)+(1)/(x^4-9)`

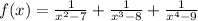
The domain is the set of inputs. So, the domain of the given function is all real numbers except those numbers for which denominator values is equal to 0.

`x^2-7=0`

`x^2=7`

`x=\pm √(7)`

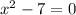
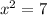
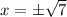
It means
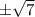`\pm √(7)` is not included in domain.

`x^3-8=0`

`x^3=8`

`x=2`

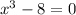
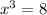
It means 2 is not included in domain.

`x^4-9=0`

`x^4=9`

`x^2=\pm 3`

`x=\pm √(3)`

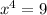
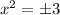
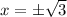
It means
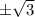`\pm √(3)` is not included in domain.

The sum of all real numbers x that are not in the domain of the function f(x) is

`Sum=-√(7)+√(7)+√(3)-√(3)+2=2`

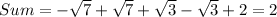
Therefore the sum of all real numbers x that are not in the domain of the function f(x) is 2.