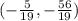Question

Which ordered pair is the solution to the system of equations?

{x+5y=−15 and y=15x+1

Answer 1

Answer:
`(-(5)/(19),-(56)/(19))`

Explanation:

Given the following system of equations:

`\left \{ {{x+5y=-15} \atop {y=15x+1}} \right.`

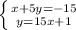
You can solve it using the Substitution Method.

You must subsitute the second equation into the first equation and then solve for "x":

`x+5(15x+1)=-15\\\\x+75x+5=-15\\\\76x=-20\\\\x=-(5)/(19)`

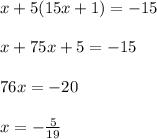
Now you must substitute the value of "x" into the second equation and evaluate, in order to find the value of "y":

`y=15(-(5)/(19))+1\\\\y=-(56)/(19)`

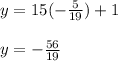
Therefore the ordered pair that is the solution to the system of equations, is:

`(-(5)/(19),-(56)/(19))`