Answer:
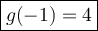
Explanation:
In this question. we would be plugging in -1 to all of the x variables.
The equation we are solving is:
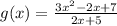
You would plug in -1 to all of the x variables.
Your equation should look like this:
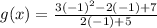
Now, you solve:
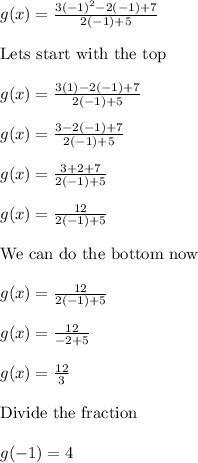
When you're done solving, you should get 4.
This means that when g is -1, the answer would be 4.
g(-1) = 4
I hope this helped you out.
Good luck on your academics.
Have a fantastic day!