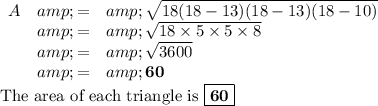Question

The perimeter of an isosceles triangle is 36. One side is 10. What are the possible lengths of the base? Find the area of the triangle.

Answer 1

`\boxed{\textbf{10 and 16; 60}}`

Explanation:

1. Length of base

There are two possibilities

(a) Base = 10

Then we have a triangle as in Fig. 1.

`\begin{array}{rcl}p & = & 2x + 10\\36 & = & 2x + 10\\26 & = & 2x\\x & = & \mathbf{13}\\\end{array}`

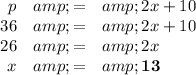
(b) Side = 10

Then we have a triangle as in Fig. 2.

`\begin{array}{rcl}p & = & x + 20\\36 & = & x + 20\\x & = & \mathbf{16}\\\end{array}\\\text{The possible lengths of the base are $\boxed{\textbf{10 and 16}}$}`

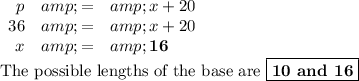
2. Area of triangle

One way to find the area of the triangle is to use Heron's formula:

`A = √(s(s - a)(s - b)(s - c))`

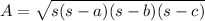
where s is the semiperimeter.

Each triangle has the same perimeter, so it also has the same semiperimeter and therefore the same area.

s = p/2 = 36/2 = 18

`\begin{array}{rcl}A & = & √(18(18 - 13)(18 - 13)(18 - 10))\\& = & √(18* 5 * 5 * 8)\\& = & √(3600)\\& = & \mathbf{60}\\\end{array}\\\text{The area of each triangle is $\boxed{\mathbf{60}}$}`