Question

What is a solution to the equation 3 / m + 3 - M / 3 - M equals m^2 + 9 / m^2-9?​

Answer 1

Answer: Last option.

Explanation:

Given the equation:

`(3)/(m+3)-(m)/(3-m)=(m^2+9)/(m^2-9)`

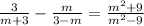
Follow these steps to solve it:

- Subtract the fractions on the left side of the equation:

`(3(3-m)-m(m+3))/((m+3)(3-m))=(m^2+9)/(m^2-9)\\\\(9-3m-m^2-3m)/((m+3)(3-m))=(m^2+9)/(m^2-9)\\\\(-m^2-6m+9)/((m+3)(3-m))=(m^2+9)/(m^2-9)`

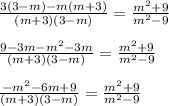
- Using the Difference of squares formula (
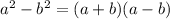`a^2-b^2=(a+b)(a-b)`) we can simplify the denominator of the right side of the equation:

`(-m^2-6m+9)/((m+3)(3-m))=(m^2+9)/((m+3)(m-3))`

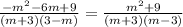
- Multiply both sides of the equation by
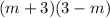`(m+3)(3-m)` and simplify:

`((-m^2-6m+9)(m+3)(3-m))/((m+3)(3-m))=((m^2+9)(m+3)(3-m))/((m+3)(m-3))\\\\-m^2-6m+9=((m^2+9)(3-m))/((m-3))`

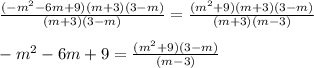
- Multiply both sides by
`m-3`:

`(-m^2-6m+9)(m-3)=((m^2+9)(3-m)(m-3))/((m-3))\\\\(-m^2-6m+9)(m-3)=(m^2+9)(3-m)`

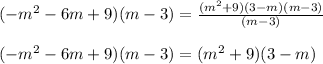
- Apply Distributive property and simplify:

`(-m^2-6m+9)(m-3)=(m^2+9)(3-m)\\\\-m^3-6m^2+9m+3m^2+18m-27=3m^2+27-m^3-9m\\\\-m^3-3m^2+27m-27+m^3-3m^2+9m-27=0\\\\-6m^2+36m-54=0`

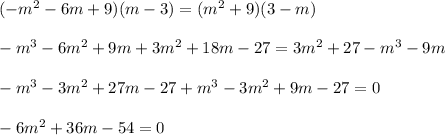
- Divide both sides of the equation by -6:

`(-6m^2+36m-54)/(-6)=(0)/(-6)\\\\m^2-6m+9=0`

- Factor the equation and solve for "m":

`(m-3)^2=0\\\\m=3`

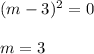
In order to verify it, you must substitute
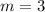`m=3` into the equation and solve it:

`(3)/(3+3)-(3)/(3-3)=(3^2+9)/(3^2-9)\\\\(3)/(6)-(3)/(0)=(18)/(0)`

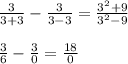
NO SOLUTION