Question

Use Simpson's Rule with n = 10 to approximate the area of the surface obtained by rotating the curve about the x-axis. Compare your answer with the value of the integral produced by your calculator. (Round your answer to six decimal places.) y = e−x2, 0 ≤ x ≤ 2

Answer 1

Split up the integration interval [0, 2] into 10 subintervals:

[0, 1/5], [1/5, 2/5], [2/5, 3/5], ..., [9/5, 2]

The left and right endpoints of the
`i`-th subinterval are, respectively,

`\ell_i=\frac{i-1}5`

`r_i=\frac i5`

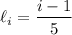
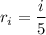
with midpoints

`m_i=\frac{\ell_i+r_i}2=(2i-1)/(10)`

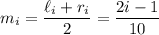
for
`1\le i\le10`.

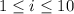Simpson's rule approximates the definite integral

`\displaystyle\int_0^22\pi e^(-x^2)\sqrt{1+(-2xe^(-x^2))^2}\,\mathrm dx=\int_0^22\pi e^(-x^2)\sqrt{1+4x^2e^(-2x^2)}\,\mathrm dx`

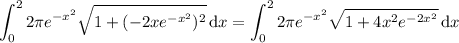
by interpolating the integrand,
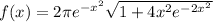`f(x)=2\pi e^(-x^2)\sqrt{1+4x^2e^(-2x^2)}`, over each subinterval with a quadratic polynomial,
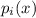`p_i(x)`, such that

`\displaystyle\int_0^2f(x)\,\mathrm dx\approx\sum_(i=1)^(10)\int_(\ell_i)^(r_i)p_i(x)\,\mathrm dx=\sum_(i=1)^(10)\frac{r_i-\ell_i}6(f(\ell_i)+4f(m_i)+f(r_i))`

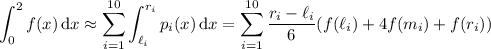
You would end up with a value of about 6.497681. Compare to the actual value of the integral, which is closer to 6.497684.