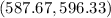Question

Use the confidence level and sample data to find a confidence interval for estimating the population mu. Round your answer to the same number of decimal places as the sample mean. A random sample of 90 light bulbs had a mean life of x overbar equals 592 hours with a standard deviation of sigma equals 25 hours. Construct a​ 90% confidence interval for the mean​ life, mu​, of all light bulbs of this type.

Answer 1

Answer:
`(587.67,596.33)`

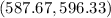
Explanation:

The confidence interval for population mean is given by :-

`\overline{x}\ \pm\ z_(\alpha/2)(\sigma)/(√(n))`

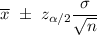
Given : Sample mean :
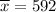`\overline{x}= 592` hours

Standard deviation
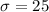`\sigma= 25` hours

Sample size : n=90, which is a large sample(n<30), so we use z-test.

Significance level:
`1-0.90=0.1`

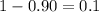
Critical value :
`z_(\alpha/2)=t_(22,0.025)=1.645`

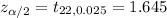
Then , the confidence interval for population mean will be :-

`592\ \pm\ (1.645)(25)/(√(90))\\\\\approx592\pm4.33\\\\=(592-4.33,592+4.33)\\\\=(587.67,596.33)`

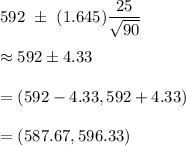
Hence, the ​ 90% confidence interval for the mean​ life
`\mu` of all light bulbs of this type. is
`(587.67,596.33)`