Answer:
(a) Normal force will be 388 N
(B) Speed of the car will be 17.94 m /sec
Step-by-step explanation:
We have given velocity of the car v = 10 m /sec
radius of the bump = 30 m
Mass of the passenger m = 60 kg
(a) When the car is at the top of the bump then normal force will be equal to weight of the body minus centripetal force
So normal force

(B) When car loose the contact then normal force will be zero
So
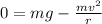
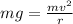
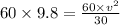
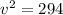
v = 17.94 m/sec