Answer with explanation:
Given : A clinical trial tests a method designed to increase the probability of conceiving a girl.
Also, in a normal case the probability of conceiving a girl is 0.5.
Let p be the proportion of girls born.
Then , we have
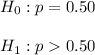
Sample size : n= 345
The sample proportion of girls born =
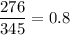
Critical value :
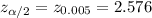
The confidence interval for population proportion is given by :_
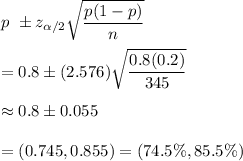
Since the confidence interval do not contains 50% that means there is increase in the probability of conceiving a girl, then it can be concluded that we have statistical evidence that the the clinical trial method increase the probability of conceiving a girl.