Question

50 points! Show your work!

Answer 1

a)19.28≈x (rounded to the nearest hundredth)

b)7.66≈x (rounded to the nearest hundredth)

c)x≈8.39(rounded to the nearest hundredth)

d)x≈36.87 (rounded to the nearest hundredth) and y=5

Explanation:

I'm going to first assume that all of these are right triangles.

If you look at the hint, it says SOHCAHTOA

This stands for the trigonometric functions

SOH tells us that sine(θ)=opposite/hypotenuse

CAH tells us that cosine(θ)=adjacent/hypotenuse

TOA tells us that tangent(θ)=opposite/adjacent

(ps. θ, or theta, stands for any angle measure)

Now, let's look at problem a.

We have the value of the hypotenuse and the value of an angle. We want to find the side opposite from the angle. So, in this case, we want to use the sine function.

sin(40)=x/30

30*sin(40)=x

19.28≈x (rounded to the nearest hundredth)

We can solve the other problems in a similar fashion.

Problem b

We have the hypotenuse, an angle measure, and we want to find the adjacent side. This is telling us to use the cosine function.

cos(40)=x/10

10*cos(40)=x

7.66≈x (rounded to the nearest hundredth)

Problem c

We have an angle measure, an adjacent value, and we want to find the opposite length, so we're going to use the tangent function.

tan(40)=x/10

10*tan(40)=x

x≈8.39(rounded to the nearest hundredth)

Problem d

We need to first solve for x, the angle measure.

We have an opposite length, an adjacent length, so we can use the tangent function to solve for the missing angle

Let's set up an equation

tan(x)=3/4

Using
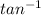`tan^(-1)` or tangent inverse to cancel out the tangent, we get

x=
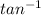`tan^(-1)`(3/4)

x≈36.87 (rounded to the nearest hundredth)

Now, let's solve for y, the hypotenuse!

Both the sine and cosine functions work, so I'm just going to pick one.

sine(36.87)=3/y

y*sin(36.87)=3

y=3/sin(36.87)

y=5

Side note: Although I rounded the angle measure, when calculating the y value, on my calculator, I did not round the value. Don't round until the end on your calculator, but it's okay to round on your paper.

PS. I used degrees for the angle measures, not radians, so if you want to retry these problems, make sure your calculator is calculating degrees, not radians, or else you might get some funky answers.

Answer 2

Explanation:

a. sin 40 =
`(x)/(10)` =
`\frac{\text{opposite side}}{hypotenuse}`

x = 10 sin 40

= 10 × 0.6427

= 6.427 units ≈ 6.43 units

b. cos 40° =
`\frac{\text{Adjacent side}}{hypotenuse}` =
`(x)/(10)`

x = 10 cos 40

= 10 × 0.766 = 7.66 units

c. tan 40 =
`\frac{\text{opposite side}}{\text{Adjacent side}}` =
`(x)/(10)`

x = 10 tan 40

= 10 × 0.839

= 8.39 units

d. tan x =
`\frac{\text{opposite side}}{\text{Adjacent side}}` =
`(3)/(4)`

x = tan⁻¹ (3/4)

= 36.87°

sin 36.87° =
`\frac{\text{opposite side}}{\text{Hypotenuse}}` =
`(3)/(y)`

0.60 =
`(3)/(y)` ⇒ y =
`(3)/(0.60)`

= y = 5 units.