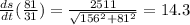Answer:
14.3
Step-by-step explanation:
The distance s as a function of time can be written as:
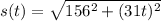
The rate of change is the derivative of d with respect to time:
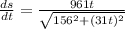
The time t when the track has been traveling for 81 miles is given by:
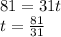
Using t in the previous equation gives: