Question

What is the sum of the geometric sequence 1, 3, 9, ... if there are 12 terms? (5 points)

Answer 1

The sum of the 12 terms is 265720

Explanation:

* Lets revise the geometric sequence

- There is a constant ratio between each two consecutive terms in the

geometric sequence

- Ex:

# 5 , 10 , 20 , 40 , 80 , ………………………. (×2)

# 5000 , 1000 , 200 , 40 , …………………………(÷5)

- The rule of the general term in the sequence is
`a_(n)=ar^(n-1)`

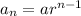
where a is the first term , r is the common ratio between each two

consecutive terms and n is the position of the term

- The sum of first n terms of a geometric series is calculated from

`S_(n)=(a(1-r^(n)))/(1-r)`

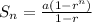
* Lets solve the problem

∵ The geometric sequence is 1 , 3 , 9 , .............

∵
`r=(a_(2))/(a_(1))`

∴
`r=(3)/(1)=3`

∵ There are 12 terms

∴ n = 12

∵ The first term is 1

∴ a = 1

∴
`S_(12)=(1(1-3^(12)))/((1-3))=265720`

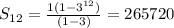
* The sum of the 12 terms is 265720