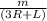Question

Solve the following equation for b. Be sure to take into account whether a letter is capitalized or not.

3Rb= −Lb+m

Answer 1

b =
`(m)/((3R + L))`

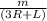
Explanation:

Solving for B in the following equation simply means to make B subject of the formula.

3Rb= −Lb+m

The first step is to add Lb to both-side of the equation, we want to cancel-out Lb from the right-hand side of the equation, so as to group all the variable containing b at the left-hand side of the equation.

3Rb + Lb = -Lb + Lb + m

On the right-hand side of the equation -Lb will cancel-out +Lb, leaving us with just m

3Rb + Lb = m

Next is to factor out b on the right-hand side of the equation

b( 3R + L) = m

Next is to divide both-side of the equation by (3R + L)

`(b(3R+L))/((3R+ L))` =
`(m)/((3R + L))`

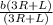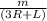
On the left-hand side of the equation, ( 3R + L ) on the numerator will cancel- out (3R+L) on the denominator leaving us with just b

b =
`(m)/((3R + L))`

Answer 2

`b=m/[3R+L]`

Explanation:

we have

`3Rb= -Lb+m`

Solve for b

That means -----> Isolate the variable b

Adds Lb both sides

`3Rb+Lb= -Lb+m+Lb`

`3Rb+Lb=m`

Factor b left side

`b[3R+L]=m`

Divide by [3R+L] both sides

`b[3R+L]/[3R+L]=m/[3R+L]`

Simplify the left side

`b=m/[3R+L]`