Answer:
The expected winnings for a person buying 1 ticket is -0.2.
Explanation:
Given : A raffle offers a first prize of $1000, 2 second prizes of $300, and 20 third prizes of $10 each. If 20000 tickets are sold at 25 cents each, find the expected winnings for a person buying 1 ticket.
To find : What are the expected winnings?
Solution :
There are one first prize, 2 second prize and 20 third prizes.
Probability of getting first prize is
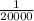
Probability of getting second prize is
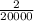
Probability of getting third prize is
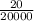
A raffle offers a first prize of $1000, 2 second prizes of $300, and 20 third prizes of $10 each.
So, The value of prizes is
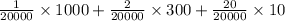
If 20000 tickets are sold at 25 cents each i.e. $0.25.
Remaining tickets = 20000-1-2-20=19977
Probability of getting remaining tickets is
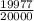
The expected value is
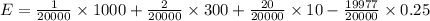
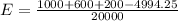
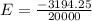
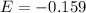
Therefore, The expected winnings for a person buying 1 ticket is -0.2.