Question

At 7:00 pm the police discovered a body in a hotel room which maintained a constant temperature of 24 degree C. At the time of discovery, the temperature of the dead body was 36 degree C. After 4 hours the temperature of the body fell to 30 degree C. Use Newton’s law of cooling to approximate the time of death. Using the formula:T – Tr = (To – Tr)e–t/tau

Answer 1

Step-by-step explanation:

According to Newton's law of cooling,

`T(t)=T_s+(T_o-T_s){e^{{-t/\tau}}`

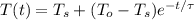
T(t) is the temperature at time t

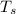`T_s` is temperature of surrounding

`k=(1)/(\tau)`

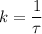
At the time of discovery, the temperature of the dead body was,
`T_o=36^(\circ)C`

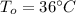
Temperature of the surrounding,
`T_s=24^(\circ)C`

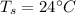
Temperature after 4 hours,
`T=30^(\circ)C`

So,
`30=24+(36-24)e^(-4t)`

On solving the above equation,

k = 0.1735

Now, put the value of k in equation (1) at T = 36 degrees C

We know that, the temperature of body before death is T(t) = 37 degrees C

`37=24+(36-24)e^(0.17t)`

On solving above equation,

t = -0.46 hour

As time can't be negative and we have taken 7:00 pm as reference time.

So, t = 27.67 minutes

So, the death of the person is at 6 : 32 pm. Hence, this is the required solution.