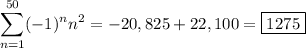Question

Determine the value of

(101*99) - (102*98) + (103*97) - (104*96) + ... + (149*51) - (150*50).

(without using calculator)​

Answer 1

101 = 100 + 1

102 = 100 + 2

103 = 100 + 3

and so on, and

99 = 100 - 1

98 = 100 - 2

97 = 100 - 3

and so on. Then the
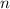`n`-th term of the sum, where
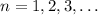`n=1,2,3,\ldots`, is

`(-1)^(n-1)(100+n)(100-n)=(-1)^n(n^2-100)`

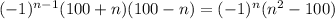
We want to compute the sum,

`(101\cdot99)-(102\cdot98)+\cdots+(149\cdot51)-(150\cdot50)=\displaystyle\sum_(n=1)^(50)(-1)^n(n^2-100)`

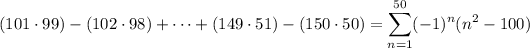
We have

`\displaystyle\sum_(n=1)^(50)(-1)^n(n^2-100)=\sum_(n=1)^(50)(-1)^nn^2-100\sum_(n=1)^(50)(-1)^n`

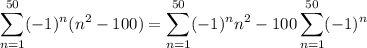
but notice that in the last sum, we're just adding the same number of 1s and -1s together, so its value is 0 and

`\displaystyle\sum_(n=1)^(50)(-1)^n(n^2-100)=\boxed{\sum_(n=1)^(50)(-1)^nn^2}`

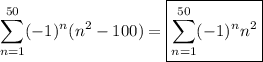
In case you're not familiar with the formula for the sum of consecutive squares, we can derive it here. Recall that

`\displaystyle\sum_(n=1)^k1=k`

`\displaystyle\sum_(n=1)^kn=\frac{k(k+1)}2`

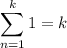
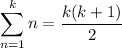
Notice that

`(n+1)^3-n^3=(n^3+3n^2+3n+1)-n^3=3n^2+3n+1`

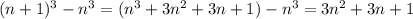
and that

`\displaystyle\sum_(n=1)^k((n+1)^3-n^3)=(2^3-1^3)+(3^2-2^3)+\cdots+(k^3-(k-1)^3)+((k+1)^3-k^3)`

`\implies\displaystyle\sum_(n=1)^k((n+1)^3-n^3)=(k+1)^3-1`

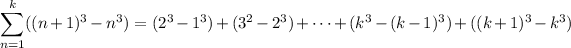
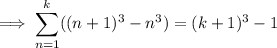
Then

`(k+1)^3-1=\displaystyle\sum_(n=1)^k(3n^2+3n+1)`

`\displaystyle\sum_(n=1)^k3n^2=(k+1)^3-1-3\frac{k(k+1)}2-k`

`\displaystyle\sum_(n=1)^kn^2={k(k+1)(2k+1)}6`

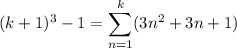
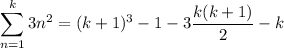
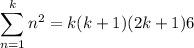
Now consider the cases where
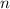`n` is either odd or even.

• If
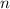  `n` is odd, we can write
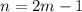  `n=2m-1`, where
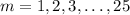  `m=1,2,3,\ldots,25`. Then

`\displaystyle\sum_(m=1)^(25)(-1)^(2m-1)(2m-1)^2=-\sum_(m=1)^(25)(4m^2-4m+1)=-\frac{2\cdot25\cdot26\cdot51}3+2\cdot25\cdot26-25`

`\displaystyle\sum_(m=1)^(25)(-1)^(2m-1)(2m-1)^2=-20,825`

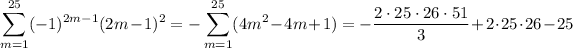
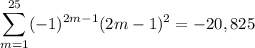
• If
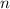  `n` is even, we can write
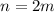  `n=2m` and so

`\displaystyle\sum_(m=1)^(25)(-1)^(2m)(2m)^2=\sum_(m=1)^(25)4m^2=\frac{2\cdot25\cdot26\cdot51}3`

`\displaystyle\sum_(m=1)^(25)(-1)^(2m)(2m)^2=22,100`

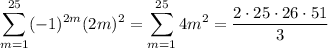
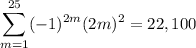
The original sum is obtained by adding the odd- and even-indexed sums together:

`\displaystyle\sum_(n=1)^(50)(-1)^nn^2=-20,825+22,100=\boxed{1275}`