Question

Paul Palumbo assumes that he will need to have a new

roof put on his house in four years. He estimates that
the roof will cost him $18,000 at that time. What
amount of money should Paul invest today at 8%,
compounded semiannually, to be able to pay for the
roof?
O $13,152.60
$24,634.80
$15,431.40
O $ 9,725.40
O none of the above​

Answer 1

$13,52.60

Explanation:

The formula to apply is

`A=P(1+(r)/(n) )^(nt)`

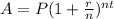
where

A= amount of money at the end

P=the amount of money to invest, principal

r=rate of interest in decimal

n=number of compoundings per year

t=time in years

Given that;

t=4 years

A=$18000

P=?

r=0.08

n=2

Substitute values in the formula

`A=P(1+(r)/(n) )^(nt) \\\\\\18000=P(1+(0.08)/(2) )^(2*4) \\\\\\18000=P(1+0.04)^8\\\\\\18000=P(1.04)^8\\\\\\18000=1.36856905041P\\`

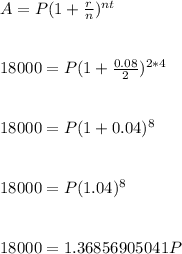
Divide both sides by 1.36856905041 to remain with P

`(18000)/(1.36856905041) =(1.36856905041P)/(1.36856905041)`

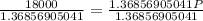
P=$13152.56