Question

Two sides of a triangle have lengths 15 cm and 19 cm. Which measurement can be the length of the third side? Question 15 options: a) 6 cm b) 4 cm c) 40 cm d) 36 cm

Answer 1

Option a and b are correct

Explanation:

According to the triangle inequalities rule, sum of two sides of triangle must be greater than the third side.

The two sides given are 15 cm and 19 cm

Their sum is: 15+19 = 34

So, the third side should be less than 34

i.e if third side is x then 0<x<34

So, from given options value of x can be 6 cm or 4 cm

Option a and b are correct.

Answer 2

Answer: The correct option is

(a) 6 cm.

Step-by-step explanation: Given that two sides of a triangle have lengths 15 cm and 19 cm.

We are to select the correct measurement that can be the length of the third side.

Let x units represents the length of the third side.

We know that the sum of the lengths of any two sides of a triangle is always greater than the length of the third side.

So, we have

`x+15>19\\\\\Rightarrow x>19-15\\\\\Rightarrow x>4~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~(i)`

`x+19>15\\\\\Rightarrow x>15-19\\\\\Rightarrow x>-4~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~(ii)`

and

`15+19>x\\\\\Rightarrow x<34~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~(iii)`

Combining inequalities (i), (ii) and (iii), we get

`4<x<34.`

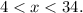
Therefore, from the given options, only 6 lies between 4 and 34.

Thus, the correct option is (a) 6 cm.