Answer:
98% confidence interval is given as [-0.204, 0.124]
Explanation:
In this question we have given
number of student in sample-1,

number of student in sample-2,

43 students in the first sample and 47 students in the second sample replied that they turned to their mother rather than their father for help
Therefore,

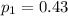
and
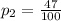

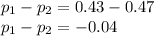
and we can determine p by using following formula,
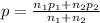 ..............(1)
..............(1)
put values of
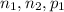 and
and
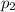 in equation (1)
in equation (1)
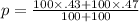
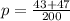
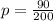

Now we can determine q by using following formula
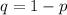 ................(2)
................(2)
put value of p in equation 2
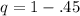
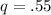
Now we can determine Standard Error of the difference between population proportions by using following formula
Standard error
=
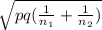 .............(3)
.............(3)
Standard error
=
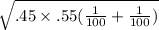
Standard error
=
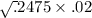
standard error=0.07035
standard error=0.0704
z- score for 98% confidence is 2.3263
Now we can determine lower limit of confidence interval by using following formula
=
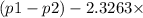 standard error
standard error
lower limit of confidence interval =
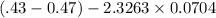
lower limit of confidence interval =
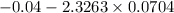 lower limit of confidence interval=-0.2038
lower limit of confidence interval=-0.2038
Similarly we can determine upper limit of confidence interval by using following formula
=
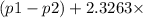 standard error
standard error
Therefore,
Upper limit of confidence interval =
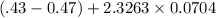
Upper limit of confidence interval =
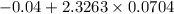
Upper limit of confidence interval= 0.1238
Therefore,
98% confidence interval is given as [-0.204, 0.124]