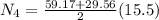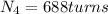Question

When switched on, the grinding machine accelerates from rest to its operating speed of 3550 rev/min in 10 seconds. When switched off, it coasts to rest in 31 seconds. Determine the number of revolutions turned during both the startup and shutdown periods. Also determine the number of revolutions turned during the first half of each period. Assume uniform angular acceleration in both cases.

Answer 1

During start total turns

`N_1 = 296 turn`

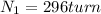
After half of the time total turns

`N_3 = (29.6 + 0)/(2)(5) = 74 turns`

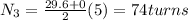
Total number of turns during it stop

`N_2 = (59.17 + 0)/(2)(31) = 917 turn`

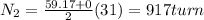
After half of the time total turns

`N_4 = 688 turns`

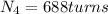
Step-by-step explanation:

Initially the machine is at rest and then starts rotating with speed 3550 rev/min

now we will have

`f = (3550)/(60) = 59.17 rev/s`

now we know that it took 10 s to reach the speed

so angular acceleration is given as

`\alpha = (\omega_f - \omega_i)/(t)`

`\alpha = (59.17- 0)/(10) = 5.917 rev/s^2`

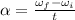
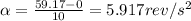
now it stops in 31 s so the angular deceleration is given as

`\alpha_2 = -(59.17)/(31) = -1.91 rev/s^2`

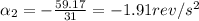
now initially number of turn to reach the given speed

`N_1 = (59.17 + 0)/(2)(10) = 296 turn`

number of turns during it stop

`N_2 = (59.17 + 0)/(2)(31) = 917 turn`

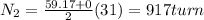
Now during startup speed after t = 5 s is given as

`\omega_1 = (5.917)(5) = 29.6 rev/s`

`N_3 = (29.6 + 0)/(2)(5) = 74 turns`

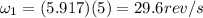
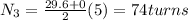
now during it stop the speed after half the time is given as

`\omega_2 = 59.17 - (1.91)(15.5) = 29.56 rev/s`

now the number of turns is given as

`N_4 = (59.17 + 29.56)/(2)(15.5)`

`N_4 = 688 turns`