Question

In a random sample of 300 women, 49% favored stricter gun control legislation. In a random sample of 200 men, 28% favored stricter gun control legislation. Construct a 98% confidence interval for the difference between the population proportions p1 - p2

Answer 1

Construct a 98% confidence interval for the difference between the population proportions p1 - p2 is ( 0.110199 and 0.309801)

Explanation:

Given data

sample n1 = 300 women

sample n2 = 200 men

control legislation f1 = 49% = 0.49

control legislation f2 = 28% = 0.28

to find out

Construct a 98% confidence interval for the difference between the population proportions p1 - p2

solution

we know difference of control legislation = f1 -f2

so difference is 0.49-0.28 = 0.21

so for 98% confidence Z value is 2.326 from standard table

and interval for difference formula is

f1 - f2 - Z
`√(f1(1-f1)/n1 + f2(1-f2)/n2)`

and

f1 - f2 + Z
`√(f1(1-f1)/n1 + f2(1-f2)/n2)`

put all these value and we get difference of population proportion are

0.49 - 0.28 - 2.326
`√(0.49(1-0.49)/300 + 0.28(1-0.28)/200)`

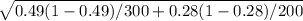
and

0.49 - 0.28 + 2.326
`√(0.49(1-0.49)/300 + 0.28(1-0.28)/200)`

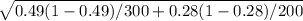
= 0.110199

and

= 0.309801

Construct a 98% confidence interval for the difference between the population proportions p1 - p2 is ( 0.110199 and 0.309801)