Step-by-step explanation:
As the given data is as follows.
Volume = 1.06 L,
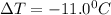
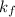 for water = 1.853 ^{0}C m, density = 1.00 g/mL
for water = 1.853 ^{0}C m, density = 1.00 g/mL
Relation between temperature change and
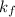 is as follows.
is as follows.
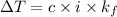
where, c = concentration
i = Van't Hoff factor
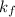 = cryoscopic constant
= cryoscopic constant
When NaCl dissolves in water then it results in formation of sodium ions and chlorine ions. In means two ions are formed so, i = 2. Therefore, putting the given values into the above formula as follows.
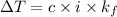
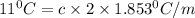
c = 2.96
As molality is defined as number of moles of solute per kg of solvent.
So, mass of NaCl that should be added is calculated as follows.
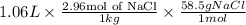
= 183.54 g
Thus, we can conclude that mass of NaCl that should be added is 183.54 g.