Question

A group of friends decided to divide the $800 cost of a trip equally among themselves. When two of the friends decided not to go on the trip, those remaining still divided the $800, 800 cost equally, but each friend’s share of the cost increased by $20. How many friends were in the group originally?

Answer 1

The number of friends were in the group originally is 10.

Explanation:

Given : A group of friends decided to divide the $800 cost of a trip equally among themselves. When two of the friends decided not to go on the trip, those remaining still divided the $800, 800 cost equally, but each friend’s share of the cost increased by $20.

To find : How many friends were in the group originally?

Solution :

Let the number of friends be 'x'.

A group of friends decided to divide the $800 cost of a trip equally among themselves.

i.e. Cost of trip for each friend is
`(800)/(x)`

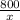
When two of the friends decided not to go on the trip, those remaining still divided the $800.

i.e. Cost of trip for each friend is
`(800)/(x-2)`

The increase in cost for each remaining friend is $20.

i.e.
`(800)/(x-2)-(800)/(x)=20`

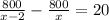
Divide the equation by 20,

`(40)/(x-2)-(40)/(x)=1`

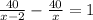
Taking LCM,

`(40x-40(x-2))/(x(x-2))=1`

`(40x-40x+80)/(x(x-2))=1`

`(80)/(x^2-2x)=1`

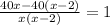
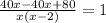
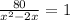
Cross multiply,

`80=x^2-2x`

`x^2-2x-80=0`

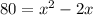
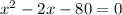
Solving by middle term split,

`x^2-10x+8x-80=0`

`x(x-10)+8(x-10)=0`

`(x-10)(x+8)=0`

`x=10,-8`

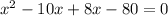
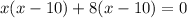
Rejecting x=-8.

Accepting x=10.

Therefore, The number of friends were in the group originally is 10.